核信息获取与处理 Chapter 3

3.1 名词解释

3.1.1 电离

当入射带电粒子与介质原子较远时，使介质的原子产生电离或激发。

3.1.2 击出

当入射 带电粒子与介质原子距离 ≈ 原子的大小（\(10^{-8}\ cm,\ 10^{-10}\ m\)）时，粒子与原子的电子相互碰撞，使电子从原子中发射出来。

3.1.3 库仑散射

当入射带电粒子与介质原子距离 ＜ 原子半径时，粒子在核库仑场中受到核库仑散射并且伴随着弱电磁辐射。

3.1.4 轫致辐射

当入射粒子为电子时，将受到核的阻尼产生出光子（连续谱X射线）。

3.1.5 切伦科夫辐射

当入射带电粒子的速度超过光在介质中的相速度时（\(v > \frac{c}{n}\)），粒子会辐射出可见光，即能量较低。

3.1.6 穿越辐射

当高速带电粒子穿过两种折射系数（折射率）不同的介质界面时，辐射出 X 光。

3.1.7 同步辐射

当电子在磁场中偏转时，相当于受到加速而产生辐射。

3.1.8 电离与激发

• 首先，入射带电粒子距离介质原子较远。

• 电离：入射带电粒子与物质原子的轨道发生库仑相互作用而损失能量，轨道电子获得能量。当电子获得的能量足以克服原子核的束缚，则电子就脱离原子成为自由电子，这就是电离。

  电离形成一对正离子与自由电子。若内壳层电子被电离后，该壳层留下空穴，外层电子跃迁来填补，同时放出特征 X 射线或俄歇电子。

• 激发：当电子获得的能量较少，不足以克服原子核的束缚成为自由电子，将跃迁至较高的能级，就是原子的激发。

  处于激发态的原子不稳定。作短暂停留后，将从激发态跃迁会基态，即退激。退激能量以荧光的形式释放。

3.1.9 介质的辐射长度

快速带电粒子因为轫致辐射导致电子平均能量减少为 1/e 的物质厚度，称为介质的辐射长度。即，

\[\langle E \rangle = E_0e^{-X/X_0} \tag{3.1}\]

3.1.10 临界能量

当辐射损失与电离损失相等时的粒子能量称为该介质的临界能量。

\[E_c = \frac{800\ (MeV)}{Z+1.2} \tag{3.2}\]

对于电子来说，

\[\begin{cases}E>E_c,&\ 轫致辐射损失为主 \\E<Ec, &\ 电离损失为主 \end{cases} \tag{3.3}\]

---

3.2 填空题

3.2.1

入射粒子能量损失的相对论上升是由于入射粒子将很大部分能量传递给少数几个电子，而这些电子又从介质中逸出，则在介质吸收层沉积的能量就接近一个常数值，这个常数值被称为费米坪。

3.2.2

在粒子能量损失大的区域有很长的尾巴延伸，这是因为产生了一个或几个能量很高的 δ 电子，这种分布通常称为朗道分布，延伸的部分能谱也被称为"朗道尾巴"。

3.2.3

电子在磁场中偏转时，相当于受到加速而产生的辐射称为同步辐射。

3.2.4

穿越辐射典型的发射角为 1/γ。

3.2.5

根据光子能量不同，可以发生不同的相互作用，在几个 keV 到几百 keV 能区，主要以康普顿效应为主。（再低主要是光电效应，更高的部分则是电子对产生效应）

3.2.6

康普顿效应是光子在自由电子上的散射，因此又称为康普顿散射。

p.s. 此处的自由电子并不能直接认为是"自由"的，电子总要受到各种力的影响，但是在 Compton 散射的过程中的电子可以近似地看作自由电子，忽略其他的作用力影响。

---

3.3 简答题

3.3.1

1. description

   由 Bathe-Bloch 公式得出粒子通过物质的平均电离能损的规律。

   \[-\frac{dE}{dx} = 4\pi N_a r^2_e m_e c^2(\frac{Z}{A})(\frac{1}{\beta^2})\Big[ \ln\big( \frac{2m_ec^2\gamma^2\beta^2}{I} \big)-\beta^2 -\frac{\delta}{2} \Big] \tag{3.4}\]

   其中，\(\beta = v/c\)，\(\gamma = 1/\sqrt{1-\beta^2}\)

2. answer

   在厚度为 \(\delta x\) 的介质层中，入射粒子的平均电离能损为：\((dE/dx)\cdot\delta x\)。

   但是只有在厚介质层时，实际的电离能损的分布才接近高斯分布。一般为朗道分布，在能量损失分布中有一不对称的尾巴—— landau 尾巴。

3.3.2

1. description

   简述混合物和化合物的电离能量损失（Bragg求和规则）。

2. answer

   混合物与化合物可以看作是由各种元素在混合物或化合物中各自的比分的薄层组成，在此情况下有 Bragg 求和规则：

   \[\frac{dE}{dx} = \sum w_j \overline{\big(\frac{dE}{dx}\big)_j} \tag{3.5}\]

   其中：

   \(\overline{\big(\frac{dE}{dx}\big)_j}\)：第 j 种元素的平均电离能量损失率，单位为 \(MeV\cdot g\ \cdot cm^{-2}\)

   \(w_j\)：第 j 种元素的权重因子

---

3.4 论述题

3.4.1 \(\gamma\) 射线与 \(X\) 射线的区别

1. 不是能量！，尽管对于大多数射线来说，\(E_X<E_\gamma\)，且 \(X\) 射线的能量一般在 keV 量级， \(\gamma\) 射线的能量则一般在 keV~MeV 量级，这仍然不能作为绝对的定性判据，因为两种射线能区有重叠。

2. 本质区别

   • \(X\) 射线：原子内层轨道电子退激发或者高能电子的轫致辐射所发出的电磁辐射。
   • \(\gamma\) 射线：原子核从激发态跃迁到低能量态时放出的射线。

3. 其他特例

   比如达到相对论性能量的高能带点粒子的穿越辐射，这种辐射也是 \(X\) 射线。它的产生机制与一般的 \(X\) 射线的机制不同，此处不再单独介绍。

   参见参考文献：【Transition Radiation】

---

3.5 计算题

3.5.1

1. description

   以 \(^{55}Fe\) 发射的 5.9 keV 的 \(X\) 射线与 Ar 气的作用过程，描述 \(γ\) 射线的光电效应。

   其中氩的壳层电子能量为：\(E_K=3.20\ keV, E_L=0.287\ keV\)。

2. solution

   

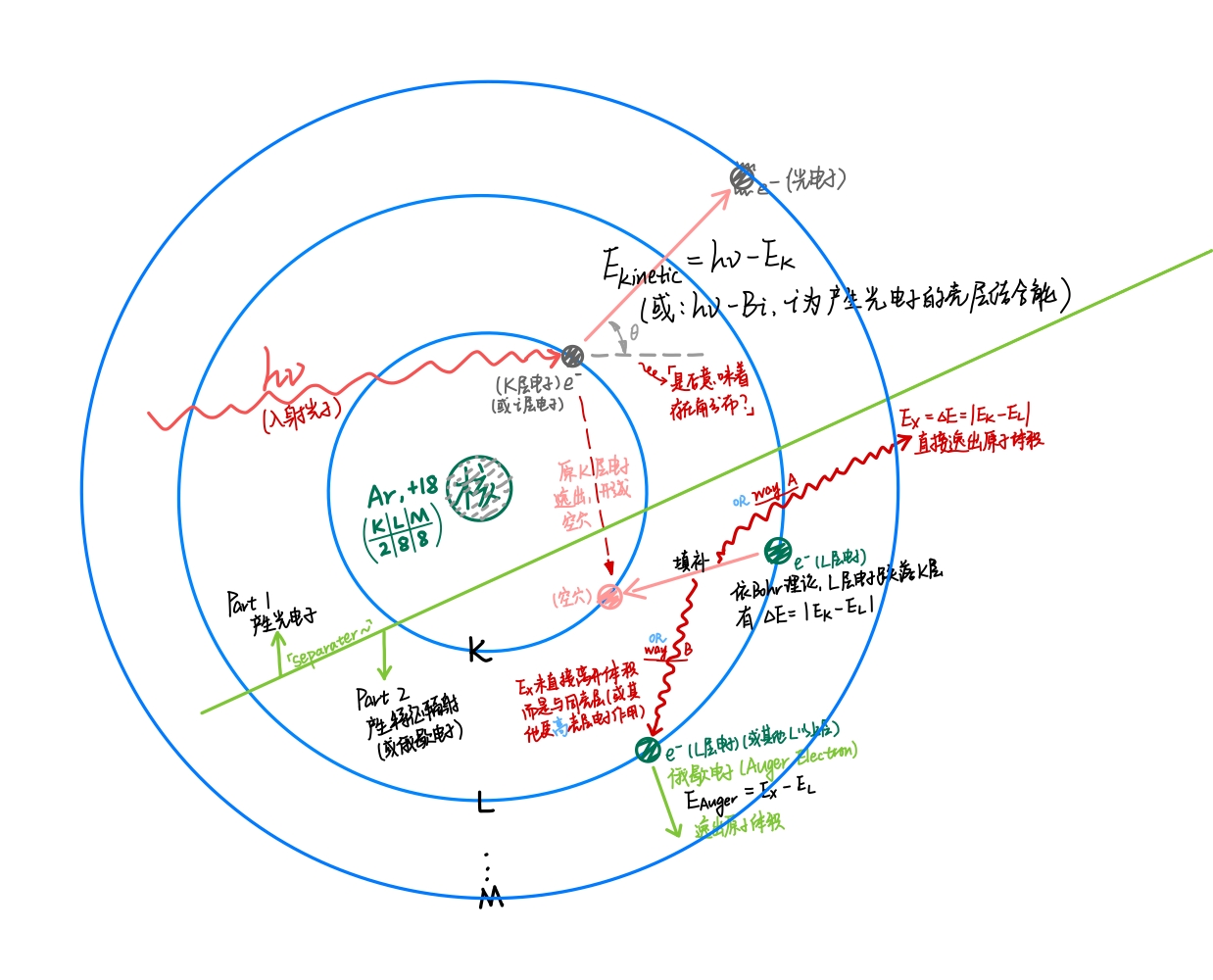
   上图描述了氩原子的光电效应。那么我们有如下的计算

   \[h\nu = E_K+E_1 \tag{3.6}\]

   其中，\(E_1\) 为光电子的动能，也是逃逸峰的峰高。

   \[E_{auger} = E_2 = E_X - E_L \tag{3.7}\] \[E_X = \vert E_K - E_L\vert \tag{3.8}\] \[\begin{align} E_1+E_2 &= (h\nu - E_K)+(E_X-E_L) \\&= h\nu-E_K+E_K-E_L-E_L \\&= h\nu - 2E_L \end{align} \tag{3.9}\]

   因此全能峰的峰高低于入射光子 \(h\nu_1\)，差值为 \(2E_L\)。

   若以下图中的数据进行详细计算：

   

   \[h\nu = 5.9\ keV,\quad E_{all} = E_1+E_2=5.33 eV\] \[E_{all}+2E_L = 5.33+2\times 0.287 = 5.904 \approx h\nu\]

   考虑到 L 壳层谱线分裂，0.04 keV 量级的差别可以抵消（？）