核信息获取与处理 Chapter 1~2
【别找了,没有第一章的提纲 ~】
2.1 名词解释
2.1.1 原子的能级
- 原子核外电子按一定轨道绕核运动时,相应的原子处于一定的能量状态;
- 一种原子绕行电子数目和运动轨道是一定的,因此,一种原子总是处于一系列确定的稳定能量状态。这一系列确定的稳定能量状态成为原子的能级,记为 \(W_i\);
- 原子的能级是量子化的,即不连续的;
- 当原子有较高能级跃迁到较低能级时,原子将以光的形式释放能量:
- 将某种原子发射的各种频率的光子按波长排列,就构成该原子的发射光谱,也即原子的光谱。
2.1.2 原子核的能级
- 中子和质子在原子核内不断运动,运动状态不同,相应的能量状态不同。原子核的不同能量状态组成原子核的能级;
- 原子核的能级是不连续的,即量子化的;
- 当原子核获得的能量准确等于两个能级的能量差时,将由低能级跃迁到高能级,处于激发态;
- 处于激发态的原子核是不稳定的,会自动从激发态跃迁到较低能态,同时以电磁辐射的形式释放出等于两个能级差的能量。
2.1.3 核辐射
不稳定的原子核衰变时发射出的,载能的,亚原子粒子。有的带电,有的不带电。
包括 \(\alpha\) 粒子、\(\beta\) 粒子、\(\gamma\) 粒子、中子、质子、裂变碎片等。
2.1.4 放射性活度
一定量的放射性核素在一定时间内发生的自发核衰变的次数与时间的比值,即 :
\[A = \frac{\Delta N_0} {\Delta t} \tag{2.2}\] 简化:亦称"衰变率",指样品在单位时间内衰变掉的原子数。
2.1.5 衰变常数
表示一个原子核在单位时间内发生衰变的几率,即
\[\lambda = \frac{-dN/dt} {N(t)} \tag{2.3}\] \[T_\frac{1} {2} = \frac{\ln2} {\lambda} = \frac{0.693} {\lambda} \tag{2.4}\]2.2 填空题
2.2.1
-
Description
重核的衰变过程中,\(\alpha\) 粒子会获得大部分衰变能。
-
Reason
衰变能并不会以热能的形式直接释放,而是转变为子核的动能。
2.2.2
-
Description
在 U 系衰变中,由 \(^{239}U \to ^{206}Pb\),其中经历了 8 次 \(\alpha\) 衰变与 6 次 \(\beta\) 衰变。
-
Reason
\[\begin{cases}\Delta A = 238 - 206 = 32 \\ \Delta Z = 92 - 82 = 10\end{cases} \tag{2.5}\]if we assume that \(x = \alpha\); \(y = \beta^-\), then
\[\begin{cases} 4x = 32 \\ 2x-y=10 \end{cases} \Rightarrow \begin{cases} x = 8 \\ y = 6 \end{cases} \tag{2.6}\]\(Q.E.D.\)
2.2.3
-
Description
在 Th 系衰变中,由 \(^{232}Th \to ^{208}Pb\),其中经历了 6 次 \(\alpha\) 衰变与 4 次 \(\beta\) 衰变。
-
Reason
\[\begin{cases}\Delta A = 232 - 208 = 24 \\ \Delta Z = 90 - 82 = 8\end{cases} \tag{2.7}\]if we assume that \(x = \alpha\); \(y = \beta^-\), then
\[\begin{cases} 4x = 24 \\ 2x-y=8 \end{cases} \Rightarrow \begin{cases} x = 6 \\ y = 4 \end{cases} \tag{2.8}\]\(Q.E.D.\)
2.3 简答题
从略
2.4 论述题
从略
2.5 计算题
2.5.1
-
Description
\(^{60}Co\) 是重要的医用放射性核素,半衰期为 5.26 年。试问 1 克 \(^{60}Co\) 的放射性强度?100 \(mCi\) 的 \(^{60}Co\) 源中有多少质量的 \(^{60}Co\) ?
-
Solution
首先给出衰变方程,
\[- \frac{dN}{N} = \lambda dt \tag{2.9}\]所以放射性活度 \(A\) 可以如下式给出,
\[A = - \frac{dN}{dt} = \lambda N \tag{2.10}\]计算衰变常数 \(\lambda\),
\[T_\frac{1}{2} = 5.26\ a \Rightarrow \lambda = \frac{\ln 2}{T_\frac{1}{2}} = 0.13175\ a^{-1} \tag{2.11}\]计算 \(^{60}Co\) 原子数,即 \(N\),
\[\frac{N}{N_A} = \frac{m}{M} \tag{2.12}\] \[N = \frac{m\cdot N_A}{M} = \frac{1\times 6.02\times 10^{23}}{60} = 1.00334\times 10^{22}\ \# \tag{2.13}\]所以对于 1 克 \(^{60}Co\),它的放射性活度为,
\[\begin{align} A = \lambda N &= 0.1375\ a^{-1}\cdot \frac{1\ a}{365\times24\times3600\ s} \cdot 1.00334\times 10^{22} \\ &= 4.192\times 10^{13}\ Bq \\ &= 1132.9\ Ci \tag{2.15} \end{align}\]对于 100 \(mCi\) 的 \(^{60}Co\) 源,它的放射性活度可以换算为,
\[100\ mCi = 3.7\times 10^9\ Bq \tag{2.16}\]为了达到这个活度,需要的粒子数为,
\[\begin{align} N = A/\lambda &= \frac{3.7\times 10^9}{0.13175\times\frac{1}{365\times 24\times 3600}} \\ &= 8.856\times 10^{17}\ \# \tag{2.17} \end{align}\]质量换算,
\[\begin{align} m = \frac{N\cdot M}{N_A} &= 0.00008827\ g \\ &= 8.827\times 10^{-5}\ g \\ &= 88.27\ \mu g \tag{2.18} \end{align}\]\(Q.E.D.\)
2.5.2
-
Description
活着的有机体中,\(^{14}C\) 对 \(^{12}C\) 的⽐与⼤⽓中是相同的,约为 \(1.3\times 10^{-12}\)。有机体死亡后,由于 \(^{14}C\) 的放射性衰变,\(^{14}C\) 含量就不断减⼩,因此,测量每克碳的衰变率就可计算出有机体的死亡时间。
现测得:新疆古⼫骸⻣的 100 g 碳的 \(\beta\) 衰变率为 900 次/min,试问古⼫已有多少年历史?( \(^{14}C\) 的半衰期按 5730 a 计算,实际应为 5700 ± 40 a)
-
Solution
-
背景:\(^{14}C\) 会发生 \(\beta^-\) 衰变,即
\[^{14}_{6}C \to ^{14}_{7}N + e^- + \bar{v_e} + 156.5\ keV \tag{2.19}\]对于现在活度仍然有 900 次/min 的古尸,它其中含有的 \(^{14}C\) 原子数应为,
\[N = \frac{A}{\lambda} = \frac{900/60}{\frac{\ln 2}{5730\times 365\times 24\times 3600}} = 3.9113\times 10^{12} \tag{2.20}\]由于上文中没有提到比值到底是质量比还是数量比,所以下面分别进行讨论计算。
-
若比值为质量比
对于刚刚死亡时的 \(^{14}C\) 含量,有
\[m_{14} = 100\times\frac{1.3\times 10^{-12}}{1+1.3\times 10^{-12}} = 1.3\times 10^{-10}\ g \tag{2.21}\] \[N_0 = \frac{m_{14}}{M} = \frac{1.3\times 10^{-10}}{14}\times 6.02\times 10^{23} = 5.59\times 10^{12}\ \# \tag{2.22}\]对上文中提到的衰变方程(2.9)求解,有
\[N(t) = N_0 \cdot e^{-\lambda t} \tag{2.23}\] \[t = \frac{\ln(N_0/N(t))}{\lambda} = \frac{\ln(\frac{5.59\times 10^{12}}{3.9113\times 10^{12}})}{\ln 2/5730} = 2952.72\ a \tag{2.24}\] -
若比值为粒子数比,则
\[N_{total} = (1+1.3\times 10^{-12})\cdot N_{12} \tag{2.25}\] \[N_{total} = N_{12} + N_{14} \tag{2.26}\] \[m_{total} = \frac{N_{12}}{N_A}\times 12 + \frac{N_{14}}{N_A}\times 14 = 100\ gram \tag{2.27}\]联立 25~27 三式,即得
\[N_{14} = 6.522\times 10^{12}\ \# = N_{0,14} \tag{2.28}\] \[t = \frac{\ln(N_0/N(t))}{\lambda} = \frac{\ln(\frac{6.522\times 10^{12}}{3.9113\times 10^{12}})}{\ln 2/5730} = 4227.73\ a \tag{2.29}\]
-
2.5.3 求 \(x\)
-
\(^{18}_8O(d,p)X\)
\[^{18}_8O+^2_1H\to ^1_1H+^{19}_8O\tag{2.30}\] -
\(X(p,\alpha)^{87}_{39}Y\)
\[^{94}_{40}Zr+^1_1H\to ^4_2He+^{87}_{39}Y\tag{2.31}\] -
\(^{123}_{52}Te(x,d)^{124}_{53}I\)
\[^{123}_{52}Te+^3_2He\to ^2_1H+^{124}_{53}I\tag{2.32}\]
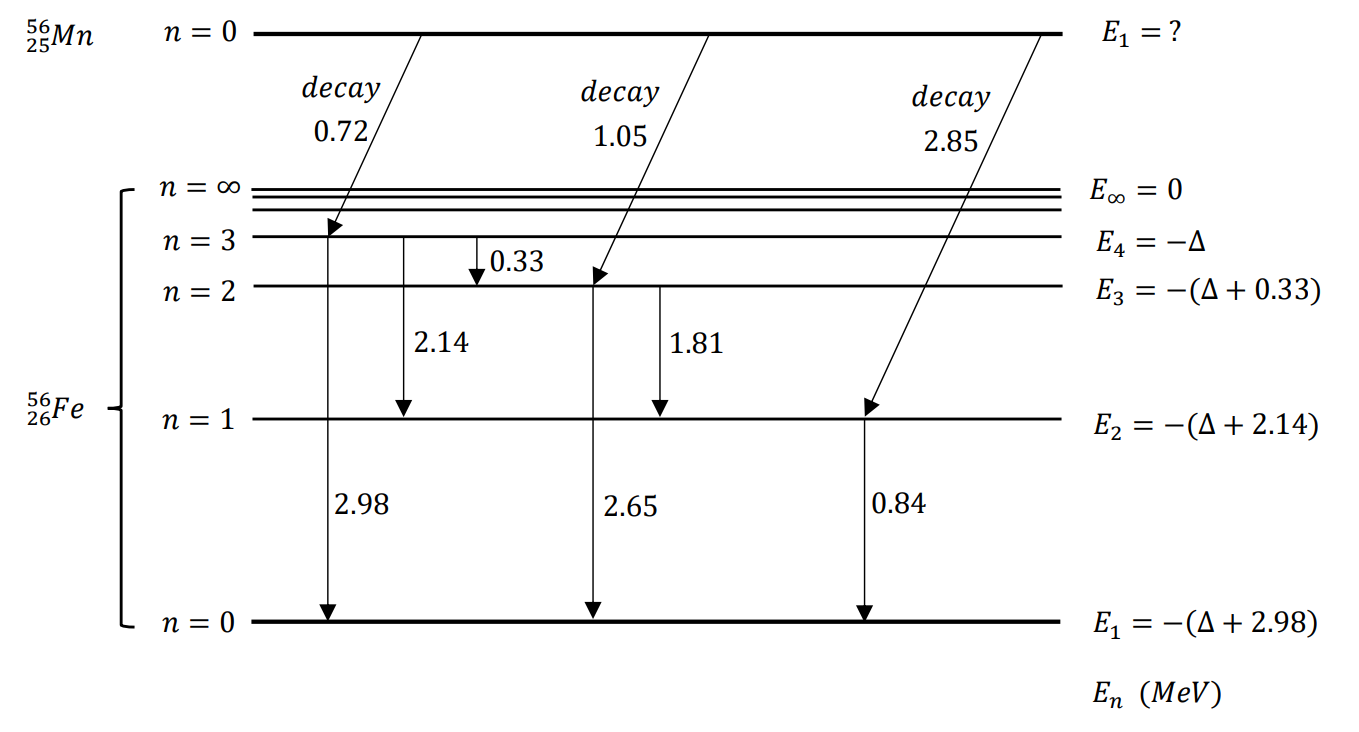
2.5.4
锰-56 核从基态进⾏ \(\beta^-\) 衰变,发射三组 \(\beta\) 粒⼦达到⼦核 铁-56 的激发态,它们的最⼤动能分别为 0.72 MeV,1.05 MeV,2.85 MeV,伴随着衰变所发射的 \(\gamma\) 射线能量有 0.84 MeV,1.81 MeV,2.14 MeV,2.65 MeV 和 2.98 MeV,试计算并画出⼦核的能级图。